先简单举个例子
假设小明每个小时只做三件事情,吃饭,睡觉,打游戏,并且他做完某件事之后会做什么事情的概率是固定的,那么我们就可以用马尔可夫链,预测他之后在每个时间段做某件事情的概率。
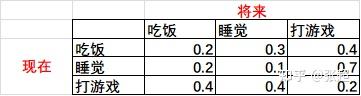
这样一来我们就得到了一个小明的做事规律的状态转移矩阵
如果小明现在在睡觉,也就是
那他下一个小时会做的事情的概率为 =
再下一个小时就是 =。。。(我就不算了)
他在第n个小时之后做这三件事情的概率,只需要用他的初始状态 ,去乘n次他的做事规律的状态转移矩阵就行。
通过这个例子,我们可以知道,马尔可夫链可以用来解决一些涉及概率和期望的数值问题,这里我们来尝试求解一下最经典的装备掉落问题:
每天可以刷四次副本,初始有20%掉落概率装备,如果没有掉落,则下一次掉落概率增加20%(掉落了则掉落概率回到20%),求平均每天可以掉落几件装备?
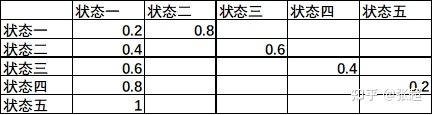
状态一指掉落概率为20%的这一状态
它有0.8的概率向状态二转移,也有0.2的概率回到自己原来的状态,即掉落装备
状态转移矩阵
初始状态
那么我们要求解的,刷四次副本后平均可以掉落几件装备,可以理解为刷每次副本掉落装备的概率之和。
我们用初始状态,去对状态转移矩阵做四次矩阵乘积,得到以下结果:
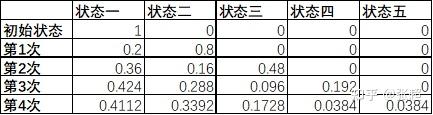
不论是从状态几,只要是回到状态一,即完成了一次装备掉落。
因此,0.2+0.36+0.424+0.4112=1.3952即为平均每天可以掉落的装备件数。